Elo vs Bradley-Terry model
Elo and Bradley-Terry are 2 ranking algorithms that can be used in tournaments. They have different use cases though:
- The Elo rating of the 2 players can be used to estimate which one of the two is the most likely to win
- You cannot use the Elo rating to rank a tournament, as the order of the games could matter.
- The Bradley-Terry model can be used to model an entire tournament, where maybe not all contestants will play against each other.
Let’s review some examples.
Elo rating system
A few days ago, a chess tournament took place. In the quarter of finals, MVL, rated 2860, played against Wesley So, rated 2741. Who should win ?
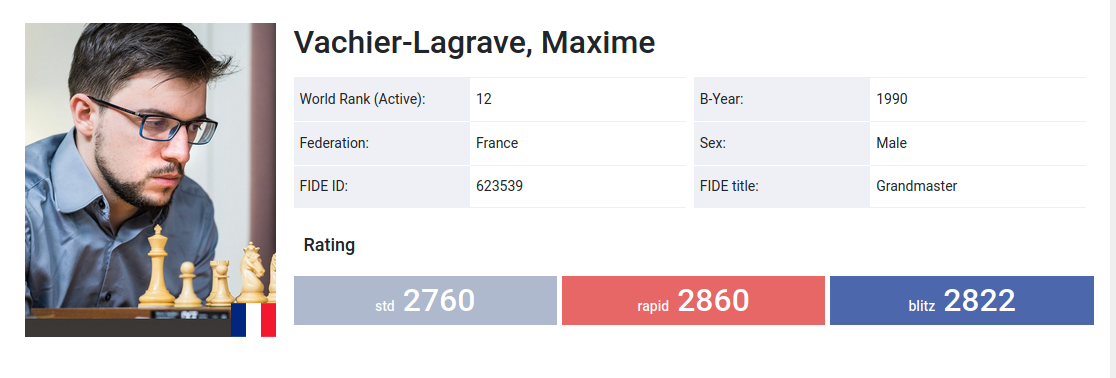
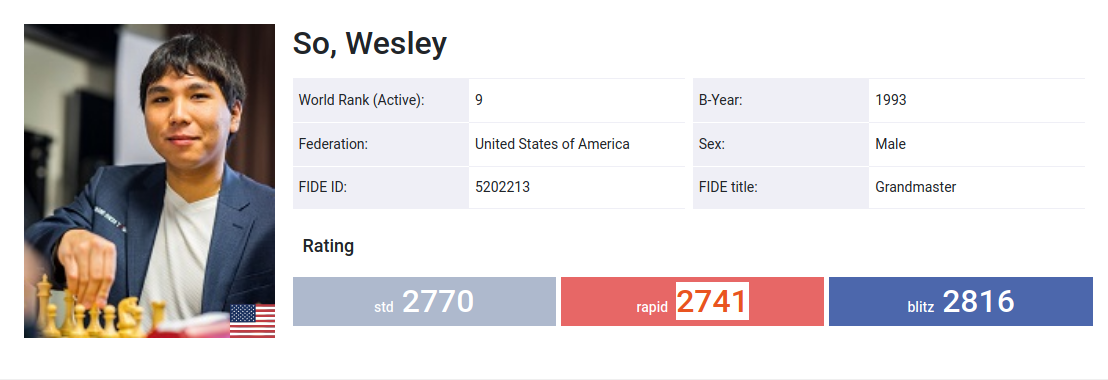
The Elo rating system answers this question with a probability:
wesley_so = 2741
mvl = 2860
D = mvl - wesley_so
probability_mvl_wins = 1/(1+10 ** (-D/400))
probability_so_wins = 1 - probability_mvl_wins
print(probability_mvl_wins)
$ python mvl-wesley-so.py
0.6648579785547648
MVL should win a game with a probability of 66%. This is not what happened though, So won ;)
Monte carlo
There are many interesting applications. One I liked is how to estimate the winner of a tournament.
It is problematic though, as you need the entire history to update the Elo ratings of the players, and the order of the operation can be an issue if you want everybody to play against each other.
The Bradley-Terry model
I came across a very interesting article about ranking chocolates. They compared 2 chocolates, and choose a winner. After many pairwise comparisons −but maybe not all possible combinations, as it can be complicated to achieve−, it is possible to use the Bradley-Terry Model in order to assign each chocolate a score.
Let’s implement Wikipedia’s example:
Suppose there are 4 teams who have played a total of 21 games among themselves.
Each team's wins are given in the rows of the table below and the opponents are given as the columns.
For example:
- Team A has beat Team B two times
- Team A lost to team B three times;
- Team A has not played team C at all
- Team A won once and lost four times against team D.
scores = [
[0, 2, 0, 1],
[3, 0, 5, 0],
[0, 3, 0, 1],
[4, 0, 3, 0]
]
What is the best team?
def update(scores: list, i:int, I:int, p: list) -> float:
"""
Given i, a computes the updated estimation for the p values
"""
assert(i < len(p))
assert(i < I)
Wi = sum(scores[i])
sum_of_ratios = 0
for j in range(I):
if i != j:
numerator = scores[i][j] + scores[j][i]
denominator = p[j]+p[i]
sum_of_ratios += float(numerator)/float(denominator)
return Wi/sum_of_ratios
def normalize(p: list) -> list:
"""
The normalization process consist in dividing
all the values by the sum of the values
"""
s = sum(p)
for i in range(len(p)):
p[i] /= float(s)
return p
def run(scores: list, p: list) -> list:
"""
Implementation of the iterative Bradley-Terry algorithm
https://en.wikipedia.org/wiki/Bradley%E2%80%93Terry_model
"""
I, J = len(scores), len(scores[0])
assert(I == J) # we need to ensure a square matrix is provided
# We update all the estimates, then we normalize
p2 = [update(scores, i, I, p) for i in range(I)]
return normalize(p2)
if __name__ == "__main__":
# Example taken from wikipedia
# https://en.wikipedia.org/wiki/Bradley%E2%80%93Terry_model#Worked_Example_of_Iterated_Procedure
# Suppose there are 4 teams who have played a total of 21 games among themselves.
# Each team's wins are given in the rows of the table below and the opponents are given as the columns.
# For example:
# - Team A has beat Team B two times
# - Team A lost to team B three times;
# - Team A has not played team C at all
# - Team A won once and lost four times against team D.
scores = [
[0, 2, 0, 1],
[3, 0, 5, 0],
[0, 3, 0, 1],
[4, 0, 3, 0]
]
# Initialize the probabilities to 1 for all the teams
p = [1]*len(scores)
for step in range(20):
p = run(scores, p)
print(f"{step}:{p}")
In this example, we run 20 iterations. Like in Wikipedia’s article, the estimates quickly converge: team D, with a score of 0.49, is the best, then Team B with a score of 0.22, then C and A are close to each others.
$ python main.py
0:[0.14803880219316745, 0.30366933783213834, 0.16448755799240827, 0.383804301982286]
1:[0.14453554168386773, 0.2802054975549539, 0.1617855814912471, 0.4134733792699312]
2:[0.14297996230400548, 0.2646246596068346, 0.15775989041916644, 0.4346354876699935]
3:[0.14200235341724074, 0.25388633939433525, 0.1541899531239827, 0.4499213540644412]
4:[0.1412633249634783, 0.2463143626319792, 0.1513737135535102, 0.46104859885103233]
5:[0.14067597059075737, 0.2408955627513518, 0.14923659258501926, 0.46919187407287166]
6:[0.14020973968641484, 0.2369781817544904, 0.14763793861341434, 0.4751741399456802]
7:[0.13984451537143508, 0.2341257543749287, 0.14644856435997544, 0.47958116589366084]
8:[0.13956217570410084, 0.2320378988770228, 0.14556542773022885, 0.48283449768864745]
9:[0.13934621155117802, 0.23050381804184814, 0.14491006871600376, 0.48523990169097003]
10:[0.1391823228782024, 0.2293734457253574, 0.14442376983163824, 0.4870204615648019]
11:[0.13905867069218494, 0.22853880178340724, 0.14406287494867756, 0.4883396525757302]
12:[0.13896576743633668, 0.22792156376950853, 0.14379500012429758, 0.48931766866985715]
13:[0.13889617893326536, 0.2274645783946562, 0.14359613717440745, 0.490043105497671]
14:[0.13884416946014816, 0.22712595130450644, 0.1434484862502272, 0.4905813929851181]
15:[0.1388053610469199, 0.22687486928370532, 0.14333884674895084, 0.49098092292042395]
16:[0.1387764372179639, 0.22668861194937212, 0.1432574258457085, 0.49127752498695537]
17:[0.13875489905663296, 0.2265503946049919, 0.1431969566833553, 0.4914977496550198]
18:[0.13873887088782177, 0.2264478000884489, 0.1431520455359051, 0.4916612834878243]
19:[0.1387269487414501, 0.22637163266363367, 0.14311868822229443, 0.4917827303726219]
Here is an example with numbers
On Gavel, that use the bradley-terry model for pairwise comparisons for a better
https://www.anishathalye.com/2016/09/19/gavel-an-expo-judging-system/
Going further
If you are interested in the maths behind ranking tournaments with many contestants but maybe not all possible comparisons will be done, you should have a look at “Designing a better judging system”
If you liked this article, you may also like my other maths and code-related articles, such as: