The birthday problem
The Birthday Problem is very well detailled on Wikipedia:
the birthday problem or birthday paradox concerns the probability that, in a set of n randomly chosen people, some pair of them will have the same birthday.
It’s counter-intuitive, but with only 23 randomly chosen people, the probability is 50%.
The math sound complex, but a Monte Carlo simulation can do wonders ; all we have to do is generate randomly birthdates, and count how often there are pairs who share a birthday.
Python was a bit slow, so I rewrote the simulation in Rust (cargo add rand). It’s still not immediate. An easy trick would be to use rayon in order to parallelize the computation, but we will find something better later on so this is not necessary.
extern crate rand;
use rand::prelude::*;
use rand::rngs::ThreadRng;
fn has_birthdays_on_same_day(nb_people: usize, rng: &mut ThreadRng) -> bool {
let mut counts = [0usize; 365];
for _ in 0..nb_people {
let day: usize = rng.gen_range(1..365);
counts[day] += 1;
if counts[day] == 2 {
return true;
}
}
false
}
fn main() {
let mut rng = rand::thread_rng();
// estimate the probability that 2 people share their birthdate,
// for 2 to 100 random people, with 10_000 iterations
let total_nb_iterations = 10_000;
for nb_people in 2..=100 {
let mut nb_birthdays_with_same_day = 0;
for _ in 0..total_nb_iterations {
if has_birthdays_on_same_day(nb_people, &mut rng) {
nb_birthdays_with_same_day += 1;
}
}
let p: f32 = nb_birthdays_with_same_day as f32 / total_nb_iterations as f32;
println!("{},{}", nb_people, p);
}
}
That’s short, but it turns out we can actually implement an analytic solution in a few lines (of Python). Since we are not performing multiple iterations, it’s in fact also much faster:
import matplotlib.pyplot as plt
nb_values = 60
p = 364/365
values = list(range(2, nb_values+1))
probas = []
for i in values:
nb_pairs = i*(i-1)/2
v = 1 - p ** nb_pairs
probas.append(v)
print("{} {:1.4f}".format(i, v))
plt.plot(values, probas)
plt.xlabel('Number of people')
plt.ylabel('Probability')
plt.title('Probability that 2 randomly selected people share a birthday')
plt.savefig("birthday-problem.png")
The results are similar:
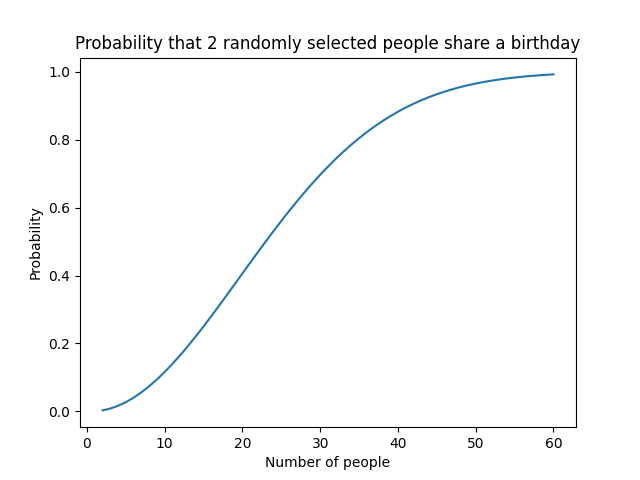
| Number of people | Probability that 2 people share their birthday |
| 2 | 0.0027 |
| 3 | 0.0082 |
| 4 | 0.0163 |
| 5 | 0.0271 |
| 6 | 0.0403 |
| 7 | 0.0560 |
| 8 | 0.0739 |
| 9 | 0.0940 |
| 10 | 0.1161 |
| 20 | 0.4062 |
| 23 | 0.5005 |
| 30 | 0.6968 |
| 40 | 0.8823 |
| 50 | 0.9653 |
| 60 | 0.9922 |